题目描述

组合数 $\binom{n}{m}$ 表示的是从 $n$ 个物品中选出 $m$ 个物品的方案数。举个例子，从 $(1,2,3)$ 三个物品中选择两个物品可以有 $(1,2),(1,3),(2,3)$ 这三种选择方法。根据组合数的定义，我们可以给出计算组合数 $\binom{n}{m}$ 的一般公式：

$$\binom{n}{m}=\frac{n!}{m!(n-m)!}$$

其中 $n!=1\times2\times\cdots\times n$；特别地，定义 $0!=1$。

小葱想知道如果给定 $n,m$ 和 $k$，对于所有的 $0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )$ 有多少对 $(i,j)$ 满足 $k \mid \binom{i}{j}$。

输入格式

第一行有两个整数 $t,k$，其中 $t$ 代表该测试点总共有多少组测试数据，$k$ 的意义见问题描述。

接下来 $t$ 行每行两个整数 $n,m$，其中 $n,m$ 的意义见问题描述。

输出格式

共 $t$ 行，每行一个整数代表所有的 $0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )$ 中有多少对 $(i,j)$ 满足 $k|\binom{i}{j}$。

数据范围

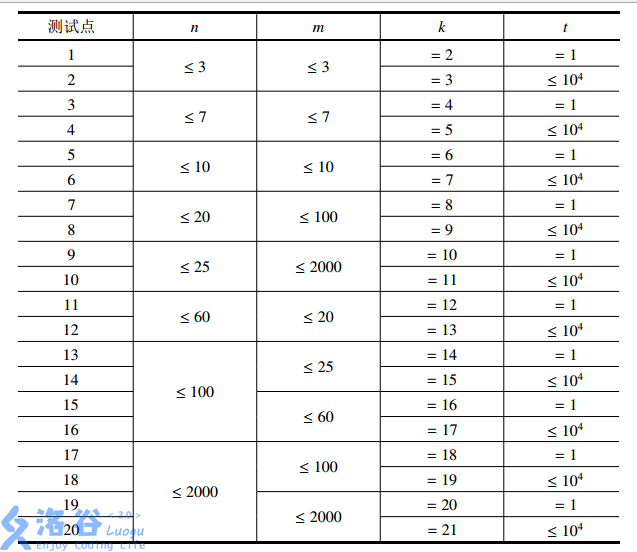
• 对于全部的测试点，保证 $0 \leq n, m \leq 2 \times 10^3$，$1 \leq t \leq 10^4$。

解题思路

数据范围超级大（含有多组数据），直接暴力求组合数肯定会 T 飞。考虑其他复杂度更低的做法。由于杨辉三角与组合数关系密切，想到了使用杨辉三角来做这道题。

杨辉三角的性质

杨辉三角第 $i$ 行的第 $j$ 个数可表示为 $\binom{i - 1}{j - 1}$ ，即从 $i-1$ 个不同元素中取 $j-1$ 个元素的组合。可以写成下面这种形式：

详细证明过程请见：【国际数学】杨辉三角和组合数。

题目求解

本题是要求有多少对 $(i, j)$（$0\leq i\leq n,0\leq j\leq \min \left (i, m \right)$ ）满足 $k \mid \binom{i}{j}$，其中 $\mid$ 表示整除 ，（详见 符号 - OI Wiki），正好符合杨辉三角的性质，所以想到使用杨辉三角来求解这道题。

由于多组数据，于是采用预处理的方法。本题不能预处理出杨辉三角后直接暴力处理多组数据，应该在预处理出杨辉三角后顺便预处理出二维前缀和，然后 $\text{O(1)}$ 查询。

数据范围很大，预处理杨辉三角时注意取模，模数为 $k$，取模后结果为 $0$ 即为整除 $k$，答案加 $1$。

正确代码

代码很清晰，应该不用写注释了。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>
#include <cmath>
#include <utility>
#include <vector>
#include <iomanip>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;

typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;

const int N = 2010;

int t, k, n, m;
int f[N][N], s[N][N];

void prework()
{
	for (int i = 0; i < N; i ++ )
		f[i][0] = 1, f[i][i] = 1;
	
	for (int i = 1; i < N; i ++ )
		for (int j = 1; j < i; j ++ )
			f[i][j] = (f[i - 1][j - 1] + f[i - 1][j]) % k;
			
	for (int i = 1; i < N; i ++ )
		for (int j = 1; j < N; j ++ )
		{
			s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1];
			if (j <= i) s[i][j] += !f[i][j];
		}
}

int main()
{
	cin >> t >> k;
	prework();

	while (t -- )
	{
		cin >> n >> m;
		cout << s[n][min(n, m)] << endl;
	}
	return 0;
}