LibreOJ-2758「JOI 2014 Final」年轮蛋糕
2022-11-21
题解
约 1.2 千字
题目描述
译自 JOI 2014 Final T3「バームクーヘン」
JOI 君马上要和妹妹 JOI 子和 JOI 美一起吃小吃。今天的小吃是他们三个人都很喜欢的年轮蛋糕。
年轮蛋糕是像下图一样呈圆筒形的蛋糕。为了把蛋糕分给三个人,JOI 君必须沿着半径方向切 刀,从而把蛋糕分成三块。然而,由于年轮蛋糕硬得像实木一样,要让刀切进去并不简单。因此,这个年轮蛋糕上事先准备了 个切口,而 JOI 君只能在有切口的位置下刀。切口按顺时针顺序编号为 到 ,对于 ,第 个切口和第 个切口之间部分的大小是 。第 个切口和第 个切口之间部分的大小是 。
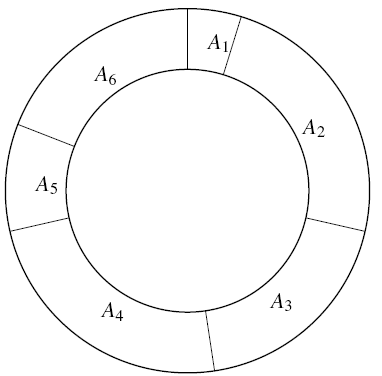
妹控的 JOI 君在把蛋糕切成 块之后,自己选走最小的一块吃掉,把剩下两块分给两个妹妹。而另一方面,JOI 君太喜欢年轮蛋糕了,只要能吃到的时候就会想吃很多很多。试求:JOI 君吃掉的蛋糕的大小至多不超过多少。
给出切口个数 和表示各部分大小的整数 ,请求出把年轮蛋糕切成 块之后最小一块大小的最大值。
Solution 1
类似题目:https://www.luogu.com.cn/problem/P1281
如果做过类似题的话,很容易发现这是一个二分。
考虑二分答案,check 里枚举第一个切口,然后贪心:后面每一刀要尽量切在往后 mid 的位置。在有序表中查找大于等于某数的第一个位置可以用二分(lower_bound)来实现。
综上所述,算法时间复杂度为 。
bool check(int mid) {
for (int i = 1; i <= n; i ++ ) { // 枚举第一刀切口
int l = lower_bound(s + i, s + i + n, mid + s[i - 1]) - s; // 贪心二分查找第二刀切口
if (l >= i + n || s[l] < mid + s[i - 1]) continue; // 第二刀切不下来,continue
int r = lower_bound(s + i, s + i + n, mid + s[l]) - s; // 二分第三刀
if (r >= i + n || s[r] < mid + s[l]) continue;
int k = s[i + n - 1] - s[r]; // 第二刀和第三刀之间的距离
if (k < mid) continue;
return true;
}
return false;
}完整代码
Solution 2
有趣的做法。
直接 while 里找第二第三刀的位置,由于后两刀切口位置移动具有单调性,时间复杂度 。
bool check(int mid) {
int p = 1, q = 1, t1 = 0, t2 = 0; // 两个指针 p 和 q
for (int i = 1; i <= n; i ++ ) { // 枚举第一刀
while (t1 < mid) {
t1 += a[p], t2 -= a[p]; // t1 增加长度,t2 提前给 t1 让位
if ( ++ p == n + 1) p = 1;
}
while (t2 < mid) { // t2 贪心增加长度
t2 += a[q];
if ( ++ q == n + 1) q = 1;
}
if (s[n] - t1 - t2 >= mid) return true;
t1 -= a[i]; // 将 t1 的第一块去掉,添加新块
}
return false;
}完整代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>
#include <cmath>
#include <utility>
#include <vector>
#include <iomanip>
#include <map>
#include <unordered_map>
using namespace std;
#define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
inline int read() {
int x = 0, f = 1; char c = getchar();
for (; !isdigit(c); c = getchar()) if (c == '-') f = -1;
for (; isdigit(c); c = getchar()) x = (x << 3) + (x << 1) + (c ^ 48);
return x * f;
}
const int N = 100010;
int n, s[N], a[N];
bool check(int mid) {
int p = 1, q = 1, t1 = 0, t2 = 0;
for (int i = 1; i <= n; i ++ ) {
while (t1 < mid) {
t1 += a[p], t2 -= a[p];
if ( ++ p == n + 1) p = 1;
}
while (t2 < mid) {
t2 += a[q];
if ( ++ q == n + 1) q = 1;
}
if (s[n] - t1 - t2 >= mid) return true;
t1 -= a[i];
}
return false;
}
signed main() {
n = read();
for (int i = 1; i <= n; i ++ ) a[i] = a[n + i] = read();
for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i];
int l = 1, r = s[n] / 3, ans = 0;
while (l <= r) {
int mid = (l + r) >> 1;
if (check(mid)) ans = mid, l = mid + 1;
else r = mid - 1;
}
printf("%lld\n", ans);
return 0;
}题目信息
| 难度 | 普及+/提高 |
| 链接 | LibreOJ-2758 |
| 来源 | LibreOJ |
LibreOJ-2758「JOI 2014 Final」年轮蛋糕
转载或引用本文时请遵守许可协议,注明出处、不得用于商业用途!