矩阵

矩阵是一种非常重要的数学对象，它通常由一个由数字排成的矩形阵列来定义。一个矩阵由若干行和若干列组成，被称为矩阵的行数和列数。一般情况下，矩阵的行数和列数分别用 $n$ 和 $m$ 表示。

矩阵中的每个元素都用一个下标表示，第 $i$ 行第 $j$ 列矩阵元素表示为 $A_{i,j}$，其中 $i$ 和 $j$ 分别表示该元素所在的行和列。矩阵中的元素可以是数字、变量或函数。

单位矩阵是指矩阵的主对角线上为 $1$ 其他位置为 $0$ 的矩阵，一般用 $\mathbf{I}$ 表示。

$$\mathbf{I}=\begin{bmatrix}1 & 0 & \cdots & 0 \\0 & 1 & \cdots & 0 \\\vdots & \vdots & \ddots & \vdots \\0 & 0 & \cdots & 1\end{bmatrix}$$

单位矩阵性质：设有一个矩阵 $A$，则有 $\mathbf{I} \times A= A$。

矩阵加法

设矩阵 $A$、$B$ 的行数和列数相等，则它们的和记作 $A+B$，其中每个元素为 $A_{i,j}+B_{i,j}$。

矩阵乘法

矩阵乘法是一种在两个矩阵之间进行的运算，其中一个矩阵的列数需等于另一个矩阵的行数。假设有两个矩阵 $A_{n \times p}$ 和 $B_{p \times m}$，它们可以被表示为：

$$A=\begin{bmatrix}a_{1,1} & a_{1,2} & \cdots & a_{1,p}\\a_{2,1} & a_{2,2} & \cdots & a_{2,p}\\\vdots & \vdots & \ddots &\vdots\\a_{n,1} & a_{n,2} & \cdots & a_{n,p}\\\end{bmatrix}\quad B=\begin{bmatrix}b_{1,1} & b_{1,2} & \cdots & b_{1,m}\\b_{2,1} & b_{2,2} & \cdots & b_{2,m}\\\vdots & \vdots & \ddots &\vdots\\b_{p,1} & b_{p,2} & \cdots & b_{p,m}\\\end{bmatrix}$$

矩阵乘积 $C_{n \times m}$ 是一个新的矩阵，它的元素 $c_{i,j}$ 定义为：

$$c_{i,j} = \sum_{k=1}^p a_{i,k}b_{k,j}$$

上式中的 $k$ 取遍所有可能的值，即 $1 \leq k \leq p$，并将乘积相加。因此，矩阵乘积的定义告诉我们，在将矩阵相乘之前，需要确保第一个矩阵的列数等于第二个矩阵的行数。

矩阵乘法不满足交换律，即 $A \times B \neq B \times A$，但它满足结合律，即 $A \times (B \times C) = (A \times B) \times C$。

例题：

• 洛谷 P3390 【模板】矩阵快速幂

• 洛谷 P1939 【模板】矩阵加速（数列）

• 洛谷 P1962 斐波那契数列

广义矩阵乘法

定义：

• $\otimes$ 有交换律：$a\otimes b=b\otimes a;$
• $\otimes$ 有结合律：$(a\otimes b)\otimes c=a\otimes(b\otimes c);$
• $\otimes$ 对 $\oplus$ 有分配律：$a\otimes(b\oplus c)=(a\otimes b)\oplus(a\otimes c);$

对于矩阵 $ A$ 和 $ B$，若 $\otimes$ 满足交换律、结合律，$\otimes$ 对 $\oplus$ 有分配律，那么我们就有广义矩阵乘法：

$$( A\times B)_{i,j}=\bigoplus_k(A_{i,k}\otimes B_{j,k})$$

广义矩阵乘法同样满足普通矩阵乘法的结合律。

常见的有：

• $\oplus$ 是 $+$，$\otimes$ 是 $\times$(普通矩阵乘法)；
• $\oplus$ 是 $\min$ 或 $\max$，$\otimes$ 是 $+$；

扩展阅读

• 「笔记」广义矩阵乘法与 DP
• 广义矩阵乘法与动态 DP 学习笔记

高斯消元

实数域上的高斯消元：

bool gauss(int n) {
	int c = 1, r = 1, t = r;
	for (; c <= n; c ++ , t = r) {
		for (int i = r; i <= n; i ++ ) if (fabs(a[i][c]) > fabs(a[t][c])) t = i;
		if (fabs(a[t][c]) < eps) continue;
		swap(a[t], a[r]);
		for (int i = n + 1; i >= c; i -- ) a[r][i] /= a[r][c];
		for (int i = r + 1; i <= n; i ++ ) {
			if (fabs(a[i][c]) > eps) {
				for (int j = n + 1; j >= c; j -- ) {
					a[i][j] -= a[r][j] * a[i][c];
				}
			}
		}
		r ++ ;
	}
	if (r <= n) {
		for (int i = r; i <= n; i ++ ) if (fabs(a[i][n + 1]) > eps) return puts("No Solution"), 0;
		return puts("Cannot Determine"), 0;
	}
	for (int i = n; i >= 1; i -- ) {
		for (int j = i + 1; j <= n; j ++ ) {
			a[i][n + 1] -= a[i][j] * a[j][n + 1];
		}
	}
	return 1;
}

异或空间上的高斯消元：

见 线性基学习笔记 #构造-高斯消元

线性空间

线性空间 是一个关于 向量加法 和 标算乘法 两个运算构成的向量集合。

• 向量加法：$a + b$。

• 标算乘法：$k \times a$，也称为数乘运算，其中 $k$ 是常数。

给定若干个向量 $a_1, a_2, a_3 \dots a_k$，若向量 $b$ 能由 $a_1, a_2, a_3 \dots a_k$ 经过 向量加法 和 标算乘法 得到，则称向量 $b$ 能被向量 $a_1, a_2, a_3 \dots a_k$ 表出，显然，所有的 $a_1, a_2, a_3 \dots a_k$ 构成一个线性空间，$a_1, a_2, a_3 \dots a_k$ 称为这个线性空间的 生成子集。

从线性空间中的任选出若干个向量，如果其中一个向量能被其他向量能表出，则称这些向量 线性相关，否则称这些向量 线性无关。

线性无关的生成子集，成为这个线性空间的 基底（极大线性无关子集）。

小提示：

• 基底不是唯一的。

• 所有基底中的向量个数都相等。

线性空间与矩阵

对于一个 $n \times m$ 的矩阵，我们可以把它的每一行看作一个长度为 $m$ 的向量，称为 行向量，矩阵的 $n$ 个行向量能够表出的所有向量构成一个线性空间，这个线性空间的维度成为 行秩，类似的，我们可以定义矩阵的 列向量 和 行秩。实际上矩阵的行秩等于列秩，他们被共同称为矩阵的 秩。

可以发现，高斯消元后得到的 简化阶梯矩阵 中的主元个数即为矩阵的秩，主元是这个线性空间的基底。

初等行变换实际上就对应了向量的两个运算。

线性基

见 线性基学习笔记。

行列式基础

定义

对于一个矩阵 $A$，其行列式定义为：

$$\det(A)=|A|=\sum_p(-1)^{\tau(p)}\prod_{i=1}^na_{i,p_i}$$

其中 $p$ 表示一个排列,所有可能的 $p$ 则是 $1$ 到 $n$ 这 $n$ 个数的全排列。$\tau(p)$ 表示一个排列 $p$ 的逆序对个数。

性质

• 交换对应矩阵的两行或两列，行列式取反
• 行列式内某一行的公因子可以提出
• 有零列的方阵，行列式为 $0$（$\det(0)=\det(0)+\det(0)$）
• 有两列相同的方阵，行列式为 $0$（$\begin{vmatrix}v_i & v_i\end{vmatrix}=-\begin{vmatrix}v_i & v_i\end{vmatrix}$）
• 将一列的 $k$ 倍加到另一列上，行列式不变（多重线性性）
• 矩阵的某一列乘 $k$ ，则行列式也乘上 $k$（多重线性性）
  • 注意： $\det(k A)=k^n \det(A)$
• $\det(A B)=\det(A) \cdot\det(B)$

二阶行列式与三阶行列式

1. 二阶行列式

形如 $\begin{vmatrix}a&b \\ c & d\end{vmatrix}$ 的行列式为二阶行列式，其行列式的值为 $ad-bc$，令向量 $p_0=(a,b),p_1=(c,d)$，则 $p_0 \times p_1=ad-bc$，这个式子恰好与二阶行列式的值相等，我们知道 $p_0 \times p_1$ 与 $p_0$，$p_1$ 张成的有向面积相等，因此二阶行列式的值等价于 $(a,b)$，$(c,d)$ 两个行向量张成的有向面积。

这个式子常用于计算一点在 $(0, 0)$ 的三角形面积，设其另外两点分别为 $A(x_1, y_1)$，$B(x_2,y_2)$，则有：

$$S_{AOB}=|\begin{vmatrix}x_1&y_1\\ x_2&y_2\end{vmatrix}|=|\vec{OA} \times \vec{OB}|=\frac{|x_1y_2-y_1x_2|}{2}$$

2. 三阶行列式

类似的，三阶行列式的值等于由三行（或三列）向量作为棱构成的平行六面体的有向体积，其计算公式为：

$$\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}=aei+dhc+bfg-ceg-bdi-fha$$

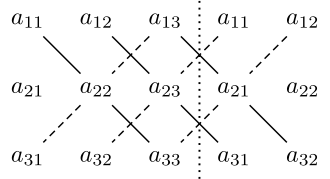
教科书上的对二阶和三阶行列式的求法常用「对角线法则」：

其中画实线的符号为正，画虚线的符号为负。

也可记为与主对角线平行为正，与副对角线平行为负，长 2 的对角线与距离较远的长 1 的对角线相乘。

特别注意：四阶行列式展开后共有 24 项，并且副对角线一项的符号为正。如果强行应用三阶行列式的「对角线法则」，不仅项数不够，副对角线一项的符号也不正确，因此三阶行列式的「对角线法则」不适用于更高阶的行列式，更高阶的行列式也不适合使用直接展开法计算。

求值

1. 对角行列式

形如 $\begin{vmatrix} a_{1,1}& 0& \cdots & 0\\ 0& a_{2,2}& \cdots & 0\\ \varvdots & \varvdots & \ddots & \varvdots \\ 0& 0& \cdots & a_{n,n}\end{vmatrix}$ 的行列式称为对角行列式。其结果为 $a_{1,1}\times a_{2,2}\cdots a_{n,n}$。

2. 三角行列式

形如 $\begin{vmatrix}a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\0&a_{2,2}&\cdots&a_{2,n}\\\varvdots&\varvdots&&\varvdots\\0&0&0&a_{n,n}\end{vmatrix}$ 的行列式被称为三角行列式，其结果与对角行列式相同。

直接根据定义求值的复杂度为 $O(n!\times n)$，不可接受。

我们可以考虑将原矩阵消元成上三角矩阵，行列式即为对角线的积。

例如有行列式 $\begin{vmatrix}2&3&5\\3&4&7\\4&3&2\end{vmatrix}$,首先可以将 $2\sim3$ 行分别加上第一行的$-\frac32,-2$ 倍，化为$\begin{vmatrix}2&3&5\\0&-\frac12&-\frac12\\0&-3&-8\end{vmatrix}$

接下来，把第三行加上第二行的 $-6$ 倍，可得 $\begin{vmatrix}2&3&5\\0&-\frac{1}{2}&-\frac{1}{2}\\0&0&-5\end{vmatrix}$。

于是原式化为了一个三角行列式。对角线乘积即为答案 $5$。

带模行列式求值

注意到 $\bmod$ 不一定为素数，很可能不存在逆元。

我们发现求解 $\gcd$ 的辗转相除法可以将一个数变为 $\gcd$，另一个数变为 $0$。

我们模仿辗转相除法。

int ans = 1, coe = 1;
for (int i = 1; i <= n; i ++ ) {
  for (int j = i + 1; j <= n; j ++ ) {
    while (a[i][i]) { // 没消掉
      int d = a[j][i] / a[i][i];
      for (int k = i; k <= n && d; k ++ ) {
        int v = mod - 1ll * d * a[i][k] % mod;
        a[j][k] = (a[j][k] + v) % mod;
      }
      swap(a[i], a[j]), coe = -coe;
    }
    swap(a[i], a[j]), coe = -coe;
  }
  if (!a[i][i]) return puts("0"), 0;
}
for (int i = 1; i <= n; i ++ ) ans = 1ll * a[i][i] * ans % mod;
ans = (ans * coe + mod) % mod;
printf("%d\n", ans);

参考资料：

• 内积和外积 OI-Wiki