P6885 [COCI2016-2017#3] Zoltan

Marton 的朋友 Cero 有一个由 $N$ 个正整数组成的数组。

首先 Cero 会在黑板上写下这个数组中的第一个数字。接下来他会在之前写下的所有数的左边或者右边写下一个数字。重复以上操作得到一个序列。

请注意，根据上述方法构造出的两个序列相同当且仅当每一个数字写下的顺序完全相同。例如，$1,1$ 可能和 $1,1$ 不同，前者的第二个数在第一个数的左边，后者的第二个数在第一个数的右边。

求这些数组成的所有序列中，最长严格递增子序列长度的最大值 $M$，以及所有最长严格递增子序列长度等于 $M$ 的序列中，最长严格递增子序列个数的总和。考虑到答案可能很大，Marton 只想知道这个数对 $10^9+7$ 取模的值。

$N\le 2\times 10^5$

Solution

问题等价于一个双端队列，可以从头或者尾插入元素，求 LIS 和 LIS 的个数。

那么可以将数分为从前面插入的和后面插入的两个子序列（设为 $S_1$，$S_2$），最终的序列就是 $S_1$ 翻转后拼上 $S_2$。

那么最终 LIS 就由前面子序列的 LDS 拼上后面子序列的 LIS 构成，由于是严格递增的，所以前面子序列的 LDS 和后面子序列 LIS 不交。

设 LIS 长度为 $ans$, LIS 数量为 $cnt$，$f_{0/1, i}, g_{0/1, i}$ 分别表示以 $i$ 为结尾（开头）的 LDS（LIS）长度、以 $i$ 为结尾（开头）的 LDS（LIS）个数。

考虑枚举 $x \in S_1 \cup S_2$，则 $len = \max\{f_{0, i}+f_{1, i}-1\}$。

由于不在 LIS 里的元素可以任意方向插入（$2^{n-ans+1}$），第一个插入的数没有方向（$2^{-1}$），所以

$cnt=\sum_{f_{0,i}+f_{1,i}-1=len}(g_{0,i}\times g_{1,i} \times 2^{n-ans+1} \times 2^{-1})$。

P7154 [USACO20DEC] Sleeping Cows P

Farmer John 有 $N$（$1≤N≤3000$）头各种大小的奶牛。他原本为每头奶牛量身定制了牛棚，但现在某些奶牛长大了，使得原先的牛棚大小不够用。具体地说，FJ 原来建造了 $N$ 个牛棚的大小为 $t_1,t_2,…,t_N$，现在奶牛的大小为 $s_1,s_2,…,s_N$（$1≤s_i,t_i≤10^9$）。

每天晚上，奶牛们都会按照某种方式寻找睡觉的牛棚。奶牛 $i$ 可以睡在牛棚 $j$ 中当且仅当她的大小可以进入牛棚（$s_i≤t_j$）。每个牛棚中至多可以睡一头奶牛。

我们称奶牛与牛棚的一个匹配是极大的，当且仅当每头奶牛可以进入分配给她的牛棚，且对于每头未被分配牛棚的奶牛无法进入任何未分配的空牛棚。

计算极大的匹配的数量模 $10^9+7$ 的结果。

Solution

考虑没有极大匹配的情况。

把牛棚和奶牛放到一个序列中排序，并离散化。

设 $f_{i,j}$ 表示考虑到第 $i$ 个位置，有 $j$ 头奶牛没有匹配上的方案数。

• 第 $i+1$ 个位置是奶牛：$f_{i, j} \to f_{i+1,j+1}$。
• 第 $i+1$ 个位置是牛棚：$f_{i, j} \times j \to f_{i+1,j-1}, f_{i,j} \to f_{i+1, j}$。

现在我们把极大的限制加上。

设 $f_{i,j,0/1}$ 表示考虑到第 $i$ 个位置，有 $j$ 头奶牛会在未来被匹配，是否有被钦定不会被匹配的奶牛的方案数。

• 第 $i+1$ 个位置是奶牛：
• 第 $i+1$ 个位置是牛棚：

P8863 「KDOI-03」构造数组

给定一个长度为 $n$ 的数组 $b$，求将一个全为 $0$ 的数组 $a$ 通过以下操作变成 $b$ 的方案数。

• 选出两个不同的下标 $1\leq i<j\leq n$，并将 $a_i$ 和 $a_j$ 同时增加 $1$。

两种方案被称之为不同的，当且仅当存在一个 $x$ 使得一种方案中第 $x$ 次操作选择的两个下标 $(i,j)$ 与另一种方案中的不同。

答案对 $\bm{998244353}$ 取模。

$1\le n\le5~000$，$1\leq b_i\le30~000$，$\sum b_i\le30~000$。

Solution

Trick：转化到网格图上的问题，类似的还有 运输货物。

操作总数 $m$ 显然是固定的，问题等价于有 $n$ 行 $m$ 列的网格，每列有两个数，每行有 $b_i$ 个数。

设 $f_{i,j}$ 表示考虑了前 $i$ 行，有 $j$ 列有两个数。

那么容易算出有一个数的列数 $k$ 和没有填数的列数 $l$。

$$k=(\sum_{x=0}^ib_x)-2j \\ l=m-j-k$$

枚举有 $u$ 个棋子放到了有 $1$ 个棋子的列，那么有转移：

$$f_{i+1,j+u} \gets f_{i,j} \times \binom{k}{u} \times \binom{l}{b_{i+1}-u}$$

时间复杂度 $O((\sum b_i)^2)$。

CF1765C Card Guessing

有 $4$ 种花色的 $4n$ 张牌，每种花色有 $n$ 张。每次从中取出一张牌，在取出第 $i$ 张牌时，你会根据最后取出的 $\min\{i - 1, k\}$ 张牌中出现次数最少的花色来猜这张牌的花色，如果有多种花色时最少的，那么你从中随机猜一种，问你猜对的期望次数是多少。

$1 \le n \le 500, 1 \le k \le 4n$。

Solution

首先根据期望线性性，期望猜对次数就等于每次猜对概率之和。

考虑 $O(n^4)$ 的做法。

在取出第 $i$ 张牌前，需要参考的牌的数量 $c = \min\{i - 1, k\}$，设四种花色的牌分别取出了 $c_1\sim c_4$ 张，满足 $c=\sum_{1 \le i \le 4} c_i$。

钦定需要参考的牌的数量和位置，剩下的牌可以随便排列，方案数为：

$$\binom{c}{c_1, c_2, c_3, c_4} \times \binom{4n - c}{n - c_1, n - c_2, n - c_3, n - c_4}$$

设 $p = \min\{c_i\}$，那么只要第 $i$ 张牌是剩下的 $4n-c$ 张牌中 $n-p$ 张的任意一张就能猜对，猜对的概率是 $\frac{n-p}{4n-c}$。

那么这一次猜测贡献到答案的期望为：

$$\binom{c}{c_1, c_2, c_3, c_4} \times \binom{4n - c}{n - c_1, n - c_2, n - c_3, n - c_4} \times \frac{n-p}{4n-c}$$

暴力枚举 $c, c_1 \sim c_4$ 中的四个，时间复杂度 $O(n^4)$。

化简上式：

$$\frac{c!(4n-c-1)!(n-p)}{c_1!(n-c_1)!\times c_2!(n-c_2)! \times c_3!(n-c_3)! \times c_4!(n-c_4)!}$$

考虑用 DP 计算 $\frac{1}{c_1!(n-c_1)!\times c_2!(n-c_2)! \times c_3!(n-c_3)! \times c_4!(n-c_4)!}$ 的和。

枚举 $p$，设 $f_{i,j,0/1}$ 表示考虑到了第 $i$ 种牌，牌的总数为 $j$，是否出现了最小值 $p$ 时的和，转移时枚举下一种牌的数量 $q$：

$$f_{i,j,0} \times \frac{1}{q!(n-q)!}\to f_{i+1,j+q,[q=p]}\\ f_{i,j,1} \times \frac{1}{q!(n-q)!}\to f_{i+1,j+q,1}$$

答案还需要乘上每种排列出现的概率 $\frac{1}{\binom{4n}{n,n,n,n}}$。

实现时可以用两个数组滚动掉第一维。

Code：https://codeforces.com/problemset/submission/1765/246423128

CF1830D Mex Tree

给定一棵 $n$ 个结点的树，点有点权，点权为 0 或 1。你需要给一种指定点权的方案，使得每一条路径的点权 $\operatorname{mex}$ 之和最大。

$n\le 2\times 10^5$，多组数据。

Solution

显然 $\operatorname{mex}$ 只可能为 $1,2,3$，我们容易产生一个贪心的想法：二分图染色，这样任意一条路径的 $\operatorname{mex}$ 值都为 $2$，但是这样不一定是最优的。

考虑已知点权的情况下，如何快速计算答案，我们发现 $\operatorname{mex}$ 当且仅当路径上只有一种颜色时不为 $2$，那么我们可以先把所有路径的贡献都算作 $2$，再把同色路径中算多的部分减掉，而大小为 $size$ 的连通块会使答案损失 $size^2 \times \operatorname{mex}$。

而一条路径是同色路径当且仅当路径起点和终点在同一个同色连通块中，所以我们可以算出每个连通块的大小，之后贡献答案。

考虑树上背包，我们设 $f_{i,j,0/1}$ 表示以 $i$ 为根的子树，连通块大小为 $j$，颜色为 $0/1$ 时答案的最小损失。

有转移：

$$f_{u,i,0}=\min_{v \in son_u}\{f_{u,i,0}+\min_j\{f_{v,j,1}\}, \min_j\{f_{u,i-j,0}+f_{v,j,0}+j(i-j)\}\} \\ f_{u,i,1}=\min_{v \in son_u}\{f_{u,i,1}+\min_j\{f_{v,j,0}\}, \min_j\{f_{u,i-j,1}+f_{v,j,1}+2j(i-j)\}\} \\$$

现在的时间复杂度为 $O(n^2)$。

由贪心可以发现答案的损失不会超过 $\frac{3}{2}n$，然而一个连通块贡献的损失是平方级别的，所以连通块的大小 $\le O(\sqrt n)$。

将第二维的大小限制到 $\sqrt n$ 后，时间复杂度 $O(n \sqrt n)$。

Code：https://www.luogu.com.cn/record/146788647

P8352 [SDOI/SXOI2022] 小 N 的独立集

给出一颗树，边权在 $[1,k]$ 之间，$\forall x \in [1,nk]$，求有多少棵树的最大权独立集的点权和为 $x$。

$n \leq 1000$，$k \leq 5$，$u_{i}, v_{i} \leq n$。

【提示】

最大权独立集问题是指：选择一个点集，使得任意两个被选择的点都没有边直接相连，并且使得所有被选择的点的点权之和最大。

Solution

对于计算子树 $u$ 的最大权独立集，只需要记录选择 $u$ 的最大权值 $p$ 和不选 $u$ 的最大权值 $q$。

这启发我们设 $f_{u,p,q}$ 表示考虑子树 $u$，两个信息分别为 $p$，$q$ 时的方案数。

$$f_{u,p_u+q_v,q_u+\max\{p_v,q_v\}}\gets f_{u,p_u,q_u} \times f_{v,p_v,q_v}$$

时间复杂度 $O(n^3k^4)$。

若 $p < q$ 时，$p$ 是没有用的，容易想到将 $p$ 的定义更改为最大独立集大小，将 $q$ 的定义更改为强制钦定 $p$ 不选时的最大独立集大小，由于选点 $u$ 的答案不会比不选点 $u$ 的答案多超过 $a_u$，所以 $p-q\le k$。

改变 $f$ 的定义，设 $f_{u,d,q}$ 表示考虑 $u$ 这个点，$p=q+d$ 时的方案数，有转移：

$$f_{u,\max\{d_u-d_v, 0\},q_u+q_v+d_v}\gets f_{u,d_u,q_u} \times f_{v,d_v,q_v}$$

状态数只有 $O(n^2k^2)$ 种，时间复杂度 $O(n^2k^4)$。

Code: https://www.luogu.com.cn/paste/omws58at

P6534 & LOJ3746 UZASTOPNI

P7142 [THUPC2021 初赛] 密集子图

给定一个边权全为 $1$ 的有向完全图

P4563 [JXOI2018] 守卫

P6563 [SBCOI2020] 一直在你身旁

有一根电线坏了。已知电线长度可能为 $1,2,\cdots,n$ 中的一个数。现在，她需要知道电线的长度。
她可以花费 $a_i$ 块钱购买长度为 $i$ 的电线。购买这根电线后，她能知道所需要的电线长度是否 大于 $i$。
保证 $a_1 \le a_2 \le \cdots \le a_n \le 10^9$。
问她至少要花多少钱才能保证知道需要电线的长度。

$$1 \le n,\sum n \leq 7100,T \leq 500$$

Solution

区间 dp，设 $f_{l,r}$ 表示已知电线长度在 $[l,r]$ 中需要的最少钱数。

$$f_{l,r}=\min_{l \le k \le r}\{\max\{f_{l,k}, f_{k+1,r}\}+a_k\}$$

看起来可以单调队列优化，但是这个 $\max$ 没法直接优化掉，考虑 $\max$ 是在 $f_{l,k}$ 取到还是在 $f_{k+1,r}$ 取到。

容易发现 $f_{l,k+1}\ge f_{l,k},f_{k+1,r}\ge f_{k+2,r}$。

那么只需要求出第一个 $f_{l,k}>f_{k+1,r}$ 的位置 $p$，就满足：

$$f_{l,r}=\begin{cases}\min\{f_{k+1,r}+a_k\},k< p\\\min\{f_{l,k}+a_k\}, k\ge p \end{cases}$$

对于 $k < p$，单调队列优化即可。
对于 $k \ge p$，由于 $a$ 序列单调不减，$p$ 就是最优的决策点。

固定 $r$，显然对于每个 $f_{l,r}$，$p$ 也是单调不增的，可以在左移 $l$ 时 $O(1)$ 求出。

时间复杂度 $O(n^2)$。

Code：https://www.luogu.com.cn/record/146201740

P3537

有 $n$ 件物品，每件物品有三个属性 $a_i, b_i, c_i\left(a_i<b_i\right)$。注意输入顺序为 $c_i, a_i, b_i$。
再给出 $q$ 个询问，每个询问由非负整数 $m, k, s$ 组成，问是否能够选出某些物品使得：

1. 对于每个选的物品 $i$ ，满足 $a_i \leq m$ 且 $b_i>m+s$。
2. 所有选出物品的 $c_i$ 的和正好是 $k$。

Solution

考虑没有 $b_i > m + s$ 限制的情况。

可以按 $a$ 排序，这样 $a_i \le m$ 的状态很容易解决。

设 $f_{i,j}$ 表示从前 $i$ 个物品中选出重量为 $j$ 的物品是否可行。

$$f_{i,j} |= f_{i-1,j-v_i}$$

现在考虑 $b_i$ 的限制：

$\forall i, b_i > m + s$ 即 $\min{b_i} > m + s$。

容易想到，设 $f_{i,j}$ 表示从前 $i$ 个物品中选出重量为 $j$ 的物品，$b_i$ 的最小值最大是多少。

$$f_{i,j} = \max\{f_{i,j}, \min\{f_{i-1,j-v_i}, b_i\}\}$$

时间复杂度 $O(nm)$。

Code：https://www.luogu.com.cn/record/120161868

CF1842E Tenzing and Triangle

有 $n$ 个点, 你需要画一些等腰直角三角形（直角边与坐标轴平行, 直角指向原点,斜边在 $x+y=k$ 上）, 画一个三角形的代价为三角形的直角边长度$\times A$ 。

对于不被任何一个三角形包含的点 $i$, 需要花费的代价为 $a_i$ 。

查询最小的花费。

$n, k \leq 2 \times 10^5$

Solution

最优解一定满足画出的三角形不交。

设一个长为 $l$ 三角形的权值为其中包含的点的权值和减去 $l \times A$，问题变为选出若干个不相交的三角形，最大化三角形的权值和，最小的花费即为所有点的点权和减去三角形的权值和。

设 $f_i$ 表示区域 $x \le i$ 的权值和，$cost(l,r)$ 为用一个三角形覆盖 $[l,r]$ 的点权和。

$$f_i=\max\{f_{i-1}, f_{j}+cost(j+1,i)-(i-j-1)\cdot A\} \\ f_i+i\cdot A=f_{j}+cost(j+1,i)+(j+1)\cdot A$$

设 $g_i = f_{i}+(i+1)\cdot A$，每转移到下一列，$g_i$ 会增加新的一行。

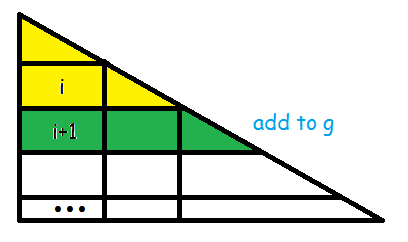
那么有转移：

$$f_i = \max\{f_{i-1}, \max_{-1\le j<i-1}\{g_j\}-i\cdot A\}$$

初始值 $f_{-1}=g_{-1}=0$。

考虑用线段树维护 $g$，每个点 $(x, y)$ 只对同一行内位于区间 $[-1,x-1]$ 的 $g$ 有贡献。

即维护前缀加，全局最大值，使用线段树维护可以做到 $O(k \log k)$，使用并查集维护可以做到 $O(k \alpha(k))$。

$O(k^2)$ Code：https://codeforces.com/contest/1842/submission/244925116

$O(k \log k)$ Code：https://codeforces.com/contest/1842/submission/244930848

CF gym 101064L The Knapsack problem

有 $N$ 种物品，第 $i$ 种重量 $w_i$，价值 $c_i$，物品有无穷个。

背包最大能承担 $m$ 的重量，最大化价值和。
$1\le N,w_i \le 10^3,1 \le m,c_i \le 10^9$。

Solution

方法 1：同余最短路

方法 2：分治

考虑将 $m$ 分为均匀的两部分，我们一直选择物品加入前半部分的背包，直到前一部分的重量超过 $\frac{m}{2}$，那么前一部分的重量在 $[\frac{m}{2},\frac{m}{2}+W]$ 之间，后一部分的重量在 $[\frac{m}{2}-W,\frac{m}{2}]$ 之间，其中 $W$ 为最大的物品重量。

我们枚举 $k \in [0,W]$，那么 $f_{m}=\max\{f_{\frac{m}{2}-k}+f_{\frac{m}{2}+k}\}$，这样是一定可以转移到最优解的。

所以算 $m$ 的答案转化为了算 $\frac{m}{2}-k,\frac{m}{2}+k$ 的答案，继续分治，直到 $m \le 2 \times W$ 时直接 dp 即可。

我们发现每层最多只会计算长度为 $W$ 的区间的 dp 值，时间复杂度 $O(W^2 \log m + Wn)$。

CF1768F Wonderful Jump

给定整数 $n$ 和长度为 $n$ 的序列 $a$ 。
从位置 $i$ 跳到位置 $j(1 \leq i \leq j \leq n)$ 需要花费 $\min\{a_i, a_{i+1}, \ldots, a_j\} \times(j-i)^2$ 枚金币。对于 $k=1,2, \cdots, n$, 求出从位置 1 经若干次跳跃后跳到位置 $k$ 需要的最小金币总数。

$a_i \le n \leq 4 \times 10^5$。

Solution

喵喵题。

设 $dp_i$ 表示从 $1$ 跳到 $i$ 的最小金币总数，容易写出 $O(n^2)$ 的转移方程：

$$dp_i = \min_{j < i}\{dp_j + (i - j) ^ 2 \times \min\{a_j, a_{j+1}, \ldots, a_i\}\}$$

这个东西既有平方项又有 $\min$，不能用常规的斜率/单调队列优化，考虑发现一些有用的性质。

性质 1

每一步覆盖的区间中的区间最小值一定在两端。

证明：$\forall i, j, 1 \le i \le j$，设区间最小值位于 $k \in (i,j)$，那么一步跳过 $k$ 的代价为 $(j-i)^2 \times a_k$，经过 $k$ 的代价为 $[(j-k)^2+(k-i)^2] \times a_k$，因为 $\forall x, y \ge 0$，有 $(x+y)^2\ge x^2+y^2$，所以经过 $k$ 比不经过 $k$ 更优。因此区间最小值一定在两端点上。

性质 2

对于一个区间最小值 $a_i$，它前面和后面的步长 $d \le \frac{n}{a_i}$。

证明：对于一段区间，如果每次以 $1$ 的距离跳，那么最多只需要 $len \times n$
对于一个最小值为 $a_i$ 的区间，跳步长为 $d$ 的一步消耗 $a_i \times d^2$，显然需要满足 $a_i \times d ^ 2 \le d \times n$ 即 $d \le \frac{n}{a_i}$。

有了以上两个性质，我们来分析一下时间复杂度：

• $\forall a_i < \sqrt{n}$，以 $a_i$ 为最小值的区间长度最大为 $n$，最多有 $\sqrt{n}$ 种数，所以时间复杂度 $O(n \sqrt{n})$。
• $\forall a_i \ge \sqrt{n}$，步长最多为 $\sqrt{n}$，时间复杂度 $O(n \sqrt{n})$。

总时间复杂度 $O(n \sqrt{n})$。

Code：https://www.luogu.com.cn/record/146740465